Las Figuras Geométricas para Niños | Árbol Abc presenta un mundo fascinante de formas y figuras, guiando a los pequeños exploradores a través de un viaje de descubrimiento geométrico. Con un enfoque en la claridad y el entretenimiento, este recurso educativo ofrece una base sólida para la comprensión de las figuras geométricas básicas y sus propiedades.
Desde las formas cotidianas que nos rodean hasta los conceptos matemáticos avanzados, Las Figuras Geométricas para Niños | Árbol Abc fomenta el pensamiento crítico y la apreciación por la belleza de la geometría.
Clasificación de figuras geométricas
Las figuras geométricas se clasifican en función de sus propiedades y características. Esta clasificación ayuda a comprender y estudiar las diferentes formas que existen.
Existen varias formas de clasificar las figuras geométricas, algunas de las más comunes son:
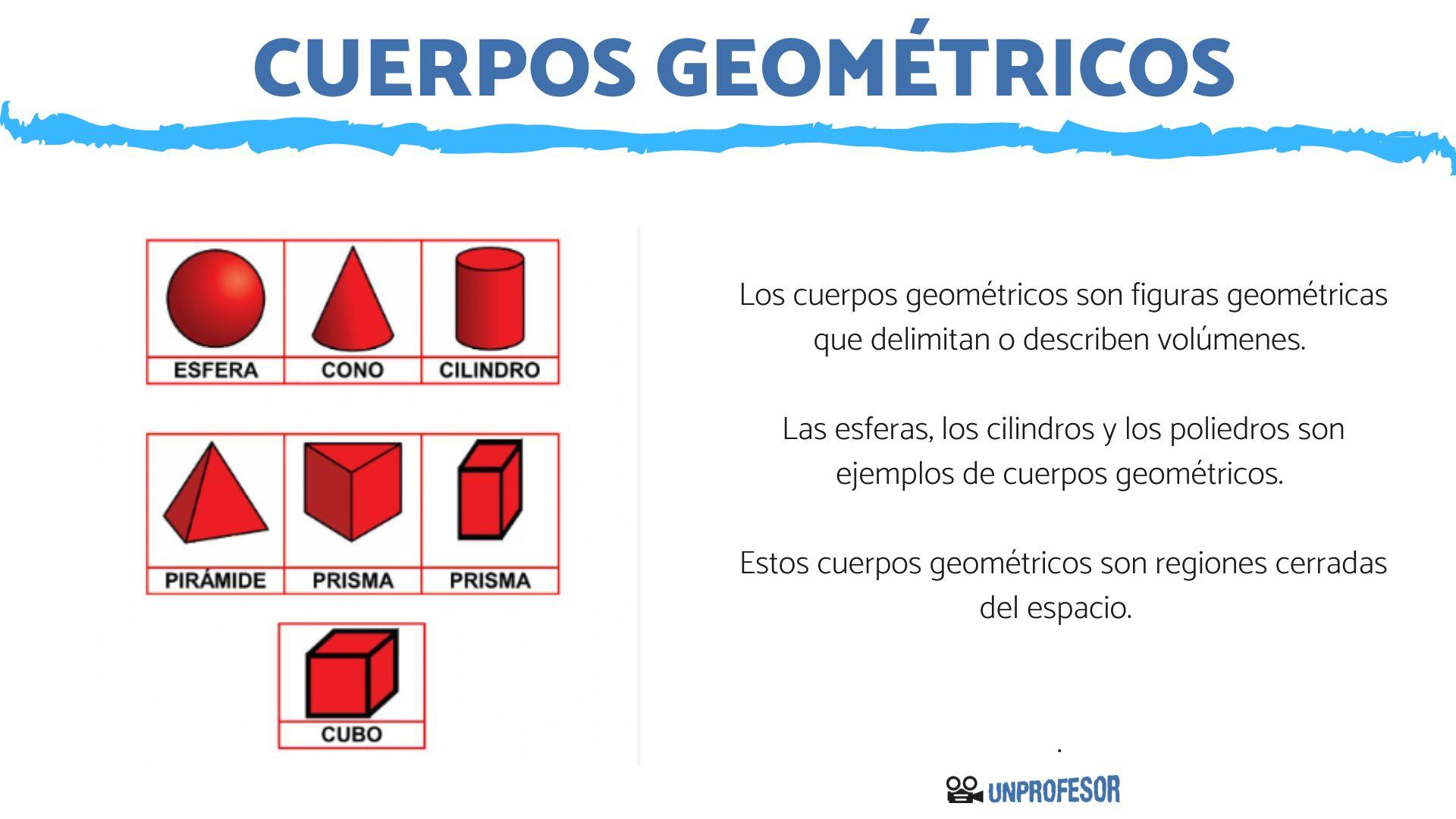
Figuras planas (2D) y figuras tridimensionales (3D)
![]()
Las figuras planas son aquellas que tienen dos dimensiones, largo y ancho. Las figuras tridimensionales, por otro lado, tienen tres dimensiones: largo, ancho y altura.
- Ejemplos de figuras planas: círculo, cuadrado, triángulo, rectángulo.
- Ejemplos de figuras tridimensionales: cubo, esfera, cilindro, cono.
Polígonos y no polígonos
Los polígonos son figuras planas formadas por segmentos de recta que se unen en puntos llamados vértices. Los no polígonos son figuras planas que no están formadas por segmentos de recta.
- Ejemplos de polígonos: triángulo, cuadrado, pentágono, hexágono.
- Ejemplos de no polígonos: círculo, elipse, estrella.
Figuras regulares e irregulares
Las figuras regulares son polígonos que tienen todos sus lados y ángulos iguales. Las figuras irregulares son polígonos que no tienen todos sus lados y ángulos iguales.
- Ejemplos de figuras regulares: cuadrado, triángulo equilátero, hexágono regular.
- Ejemplos de figuras irregulares: triángulo escaleno, trapecio, pentágono irregular.
Propiedades de las figuras geométricas
Las figuras geométricas poseen características específicas que permiten clasificarlas y estudiar sus propiedades. Estas propiedades se dividen en dos grupos principales: propiedades de figuras planas y propiedades de figuras tridimensionales.
Entre las propiedades de las figuras planas se encuentran el perímetro y el área, mientras que las figuras tridimensionales poseen propiedades como el volumen y la superficie. Además, tanto las figuras planas como las tridimensionales pueden exhibir simetría y transformaciones geométricas.
Perímetro y área de figuras planas
El perímetro de una figura plana es la suma de las longitudes de todos sus lados. El área, por otro lado, representa la cantidad de espacio que ocupa la figura dentro de un plano bidimensional.
- Para calcular el perímetro de un cuadrado, se multiplica la longitud de un lado por 4.
- El área de un triángulo se calcula multiplicando la base por la altura y dividiendo el resultado entre 2.
- El perímetro de un círculo se calcula multiplicando el diámetro por π (pi).
Volumen y superficie de figuras tridimensionales
El volumen de una figura tridimensional mide la cantidad de espacio que ocupa en el espacio tridimensional. La superficie, en cambio, representa el área total de la superficie de la figura.
- El volumen de un cubo se calcula multiplicando la longitud de un lado por sí misma tres veces.
- La superficie de una esfera se calcula multiplicando el cuadrado del radio por 4π.
- El volumen de un cono se calcula multiplicando el área de la base por la altura y dividiendo el resultado entre 3.
Simetría y transformaciones geométricas, Las Figuras Geométricas Para Niños | Árbol Abc
La simetría se refiere a la propiedad de una figura de permanecer inalterada bajo ciertas transformaciones. Las transformaciones geométricas son operaciones que se pueden realizar sobre una figura sin alterar su forma o tamaño.
- Una figura es simétrica si tiene un eje de simetría, que es una línea que divide la figura en dos partes iguales.
- Las transformaciones geométricas incluyen traslaciones (desplazamientos), rotaciones (giros) y reflexiones (volteos).
- La simetría y las transformaciones geométricas son fundamentales para comprender las propiedades de las figuras y sus aplicaciones en diversas áreas, como el arte, la arquitectura y la ingeniería.
Aplicaciones de las figuras geométricas: Las Figuras Geométricas Para Niños | Árbol Abc

Las figuras geométricas tienen innumerables aplicaciones en diversos ámbitos de nuestra vida diaria. Desde la arquitectura y el diseño hasta el arte y la ciencia, estas formas básicas desempeñan un papel crucial en la configuración de nuestro mundo.
Arquitectura y diseño
En arquitectura, las figuras geométricas forman la base de los planos de construcción y el diseño de estructuras. Las formas rectangulares y cuadradas se utilizan ampliamente para crear espacios habitables, mientras que las formas curvas y triangulares se emplean para añadir interés visual y mejorar la estabilidad estructural.
Arte y manualidades
En el mundo del arte y las manualidades, las figuras geométricas sirven como elementos esenciales de composición y expresión. Los artistas utilizan formas geométricas para crear patrones, texturas y profundidad en sus obras. Desde las formas orgánicas de la naturaleza hasta las líneas rectas y los ángulos de la arquitectura moderna, las figuras geométricas ofrecen un lenguaje visual versátil para transmitir ideas y emociones.
Ciencia y tecnología
Las figuras geométricas son fundamentales en muchos campos científicos y tecnológicos. En física, se utilizan para modelar el movimiento y la fuerza. En ingeniería, se emplean para diseñar puentes, aviones y otros objetos que deben soportar cargas y tensiones. Incluso en campos como la medicina y la biología, las figuras geométricas ayudan a los científicos a comprender la estructura y función de los organismos vivos.
